Cinetica enzimatica

Cinetica enzimatica

Le reazioni chimiche che avvengono nelle cellule sono catalizzate dagli enzimi. Questi importanti catalizzatori sono specifici per una particolare reazione. Nel loro complesso, sono estremamente versatili nel senso che alcune migliaia di enzimi ora conosciuti, portano avanti tutte quelle reazioni diverse indispensabili per la cellula come ad esempio: l'idrolisi, la polimerizzazione, le ossidoriduzioni etc. Inoltre, queste proteine non si comportano da superfici passive su cui avvengono le reazioni, ma sono piuttosto complesse macchine molecolari che operano mediante una serie di meccanismi molto diversi tra loro.
L'EQUAZIONE DI MICHAELIS-MENTEN
Lo studio della cinetica enzimatica è iniziato nel 1902, quando Adrian Brown riportò una sua ricerca sulla velocità di idrolisi del saccarosio catalizzata dall'enzima del lievito invertasi (noto ora come β-fruttofuranosidasi): saccarosio + H2O→glucosio + fruttosio. Egli dimostrò che quando la concentrazione del saccarosio è molto più alta di quella dell'enzima, la velocità della reazione diventa indipendente dalla concentrazione di saccarosio; cioè, la velocità è di ordine zero rispetto al saccarosio. Brown pensò quindi che la reazione complessiva fosse composta da due reazioni elementari, in cui il substrato formava prima un complesso con l'enzima che successivamente si decomponeva a prodotti ed enzima libero:       

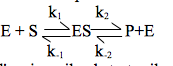
Qui, E, S, ES e P indicano rispettivamente l'enzima, il substrato, il complesso enzima-substrato e i prodotti. Secondo questo modello, quando la concentrazione del substrato diventa sufficientemente elevata da convertire completamente l'enzima nella forma ES, la seconda tappa della reazione diventa quella che limita la velocità e la reazione complessiva è insensibile ad ulteriori aumenti nella concentrazione del substrato. L'espressione generale della velocità di questa reazione è:        
v = d[P]/dt = k2[ES]
La velocità complessiva di produzione di [ES] è data dalla differenza tra le velocità delle reazioni elementari che portano alla sua formazione e che determinano la sua scomparsa:                  
d[ES]/dt = k1[E][S] – k-1[ES] – k2[ES]
Questa equazione non può essere esplicitamente integrata senza effettuare alcune assunzioni semplificatrici. Le due possibilità sono:
1.Assunzione di equilibrio. Nel 1913, Leonor Michaelis e Maude Menten assunsero che k-1>>k2, cioè che la prima tappa della reazione potesse raggiungere l'equilibrio. Ks = k-1/k1 = [E][S]/[ES]; Ks rappresenta la costante di dissociazione della prima tappa della reazione enzimatica. Dopo questa assunzione, l'equazione d[ES]/dt = k1[E][S] – k-1[ES] – k2[ES] può essere integrata.
2.Assunzione dello stato stazionario. Con l'eccezione della parte iniziale della reazione (fase transitoria), che avviene in pochissimo tempo dopo aver mescolato l'enzima con il suo substrato, [ES] rimane costante fino a che il substrato non comincia ad esaurirsi. Di conseguenza, la velocità di sintesi di ES deve essere uguale alla velocità di demolizione per quasi tutto il tempo della reazione; [ES] resta cioè in uno stato stazionario. Si può assumere quindi che [ES] rimane costante e quindi: d[ES]/dt = 0.
I valori di [ES] e di [E] non sono in genere facilmente quantificabili per via diretta, ma la quantità di enzima totale [E]T è invece sempre nota:      [E]T = [E] + [ES]  
A questo punto, l'equazione di velocità della nostra reazione enzimatica può essere derivata combinando l'equazione d[ES]/dt = k1[E][S] – k-1[ES] – k2[ES] con l'assunzione dello stato stazionario, l'equazione d[ES]/dt = 0 con [E]T = [E] + [ES], si ha:
k1([E]T – [ES])[S] = (k-1+k2)[ES]
che dopo opportuni riarrangiamenti diventa:
[ES](k-1+k2+k1[S]) = k1[E]T[S]
Dividendo entrambi i termini per k1 e risolvendo per [ES],
[ES] = [E]T[S]/KM+[S]
dove KM, nota come costante di Michaelis, è definita da:                              
KM = k-1+k2/k1
La velocità iniziale della reazione, in base a [E]T ed [S], sarà:
v0 = (d[P]/dt)t=0 = k2[ES] = k2[E]T[S]/KM+[S]
L'uso della velocità iniziale invece che la velocità nel suo complesso minimizza alcune complicazioni, quali gli effetti dell'eventuale reversibilità delle reazioni, l'inibizione dell'enzima da parte del prodotto e la possibile progressiva inattivazione dell'enzima stesso.
La velocità massima di una reazione, invece, viene raggiunta solo quando l'enzima viene saturato da un'elevata concentrazione del substrato, cioè è completamente nella forma [ES]:
Vmax = k2[E]T
Quindi combinando v0=(d[P]/dt)t=0=k2[ES]=k2[E]T[S]/KM+[S] all'equazione Vmax= k2[E]T otteniamo:                                           
v0 = Vmax[S]/KM+[S]
Quest'ultima espressione, l'equazione di Michaelis-Menten, è alla base della cinetica enzimatica e descrive un iperbole rettangolare. Quindi, possiamo concludere dicendo che la velocità di una reazione enzimatica in qualsiasi istante, è determinata dal rapporto fra due costanti Vmax e KM e la concentrazione del substrato in quell'istante.

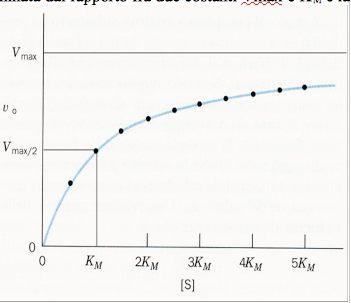
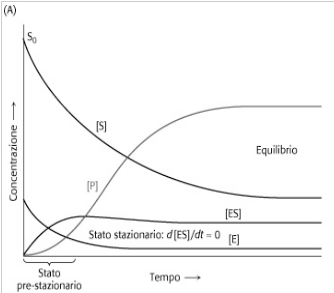
La costante di Michaelis, KM, operativamente può essere definita in modo molto semplice. Alla concentrazione di substrato in cui [S]=KM, dall'equazione v0=Vmax[S]/KM+[S] si ottiene che v0 = vmax/2 e quindi, KM corrisponde alla concentrazione di substrato a cui la velocità della reazione è metà di quella massima. Se un enzima, conseguentemente, ha una KM con un valore piccolo, esso arriverà alla massima efficienza catalitica ad una concentrazione di substrato piuttosto piccola. Il valore di KM, comunque, varia considerevolmente con il tipo di enzima e con la natura del substrato. Anche la temperatura e il pH possono influenzare il valore della costante. La costante di Michaelis può essere espressa come:                   
KM = k-1/k1+k2/k1 = Ks+k2/k1
poiché Ks è la costante di dissociazione del complesso di Michaelis, se Ks diminuisce, aumenta l'affinità dell'enzima per il substrato. La KM è anche una misura dell'affinità dell'enzima per il suo substrato, se il rapporto k2/k1 è molto piccolo in confronto a Ks, cioè k2>k-1.