Definizione dell'Indice di Herfindhal – Hirschman
L’indice HH dipende sia dalla disuguaglianza delle quote di mercato che dal numero delle imprese (N). Esso si calcola sommando i quadrati dei valori che esprimono la dimensione di ogni singola unità considerata.
Questo indicatore fa la sommatoria per i che varia da 1 a 9 (nel nostro caso) di tutte le quote di mercato al quadrato. 
Supponiamo di avere un settore con 3 imprese. Se le guardo così non c’è concentrazione, gli addetti sono quasi equi distribuiti.
Per valutare il risultato di un indice devo avere un campo di variazione. Il campo di variazione di questo indice è da 1/N a 1.
N nel nostro caso è 3, 1/N = 0,33. Più l’indice HH si avvicina a 1/N più c’è assenza di concentrazione.
Nel secondo esempio sicuramente c’è concentrazione. Faccio lo stesso procedimento. Il campo di variazione va da 0,25 (minima concentrazione) a 1 (massimo concentrazione. Lo 0,57 indica della concentrazione nel mercato.
Questo indicatore tiene conto della numerosità e della disuguaglianza. L’elevamento al quadrato fa pesare di più l’impresa più grande. Più il valore è grande, più l’elevamento al quadrato da più peso alle imprese più grandi. 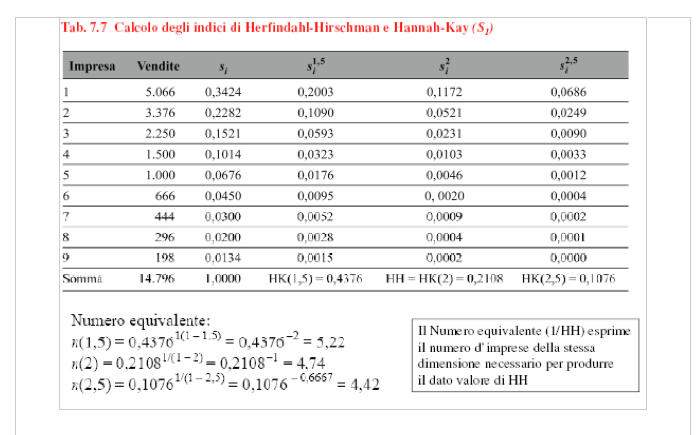
L’indice HH viene indicato nell’ultima colonna.
Nel momento in cui HH studiano questo indicatore, altri economisti HANNAH – KAY dicono perché elevare al quadrato, si può elevare ad un altro valore.
Se so che il settore è molto diseguale, è meglio utilizzare un elevamento a potenza più alto, perché voglio che la diseguaglianza sia evidenziato dall’elevamento a potenza. Questo indice è esattamente l’indice di HH non predeterminando a priori l’elevamento al quadrato, è compito dell’economista che fa l’analisi decidere il valore della potenza.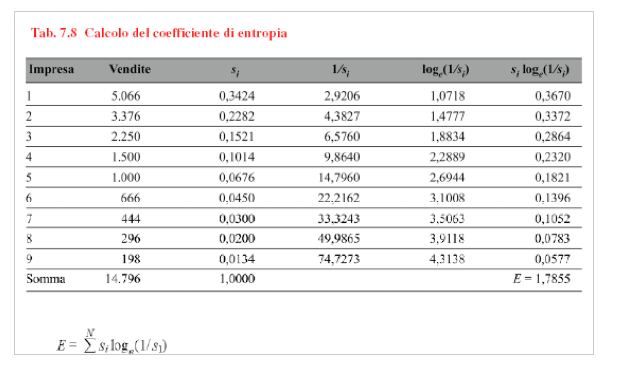
Cambia solo il metodo di ponderazione. La formula base è sempre la somma delle imprese di mercato.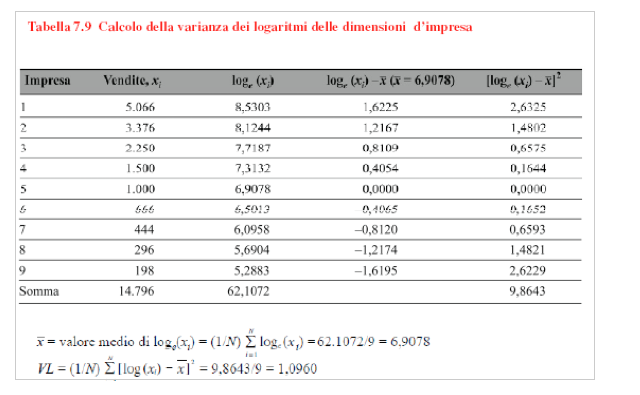
Continua a leggere:
- Successivo: Calcolo della curva di Lorenz e coefficiente di Gini
- Precedente: Definizione del rapporto di concentrazione (Cn)
Dettagli appunto:
-
Autore:
Valentina Minerva
[Visita la sua tesi: "Le strategie di contrasto al fenomeno del riciclaggio: tutela penale e tutela amministrativa"]
- Università: Università Cattolica del Sacro Cuore di Milano
- Facoltà: Economia
- Esame: Economia industriale
- Docente: Pontarollo Enzo
Altri appunti correlati:
- Microeconomia
- Diritto dell'Impresa
- Riorganizzazioni Aziendali
- Diritto Commerciale
- Economia aziendale
Per approfondire questo argomento, consulta le Tesi:
- Accordi orizzontali: M&A e JV. Il caso Bombardier: analisi di una strategia
- Politica della concorrenza e fusioni orizzontali: analisi di un caso
- M&A DOs and DONTs. Un modello di valutazione ex-ante. Il caso Finmeccanica
- Le concentrazioni tra imprese nel diritto comunitario della concorrenza
- Franchising e normativa antitrust
Puoi scaricare gratuitamente questo appunto in versione integrale.

