Calcolo della curva di Lorenz e coefficiente di Gini
Sull’asse delle ascisse si hanno le % cumulate delle imprese, ordinate a partire dalla più piccola (pi) e sulle ordinate le % cumulate della dimensione di tutte le imprese (qi).
Se tutte le imprese hanno la stessa dimensione la curva di Lorenz è la retta a 45°(OCA).
Se, invece, vi è disparità dimensionale fra le imprese, la curva di Lorenz si colloca al di sotto della retta di equi distribuzione.
La concentrazione sarà tanto maggiore quanto maggiore è la differenza (pi - qi).
La bisettrice viene chiamata retta di equi distribuzione. Quando la variabile che considera la numerosità aumenta, e aumenta anche la variabile di riferimento, sono sulla retta di equi distribuzione.
L’area sotto la retta di equi distribuzione viene chiamata area di concentrazione e mi da delle indicazioni su questa.
Sull’asse delle ascisse si hanno le percentuali cumulate delle imprese, che sono pi, ordinate a partire dalla più piccola. Sull’asse delle ordinate abbiamo le percentuali cumulate di un’altra variabile, qi. Se tutte le imprese hanno le stesse dimensioni siamo sulla curva di Lorenz. Se invece vi è disparità dimensionali tra le imprese, la curva di Lorenz si colloca al di sotto della retta di concentrazione, e si crea l’area di concentrazione.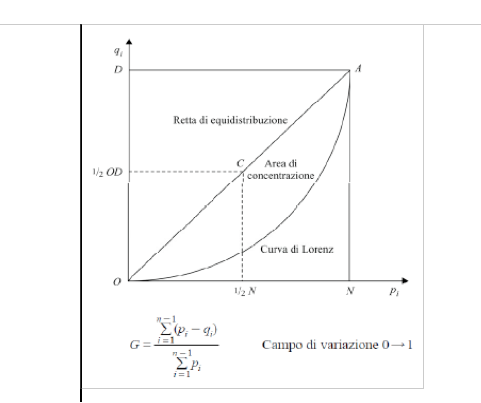
Al numeratore c’è la somma delle differenze tra pi e qi. Se non esiste differenza siamo sulla retta, quando c’è differenza invece c’è concentrazione.
Al denominatore si tiene conto del valore massimo che questo indicatore può raggiungere.
Prendo n-1 perché a n la differenza è 0. 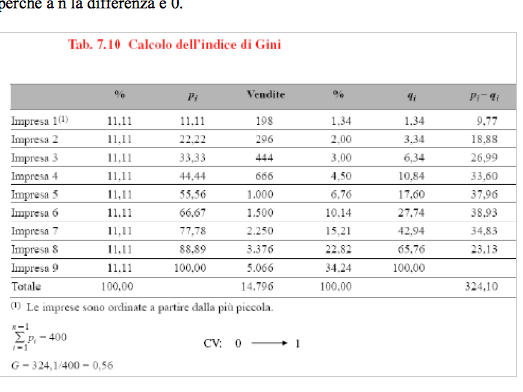
Il rapporto di concentrazione va dalla più grande alla più piccola, qui partiamo dalla più piccola alla più grande, se no verrebbe una curva convessa e non concava.
L’indice di Gini varia da 0 a 1.
CURVA DI LORENZ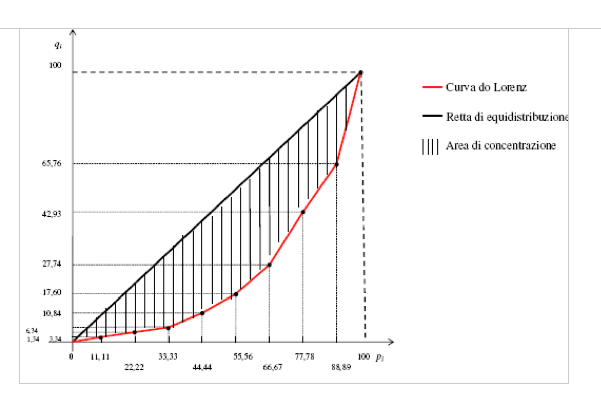
Continua a leggere:
- Successivo: Calcolo della struttura più competitiva: Esercizio 1
- Precedente: Definizione dell'Indice di Herfindhal – Hirschman
Dettagli appunto:
-
Autore:
Valentina Minerva
[Visita la sua tesi: "Le strategie di contrasto al fenomeno del riciclaggio: tutela penale e tutela amministrativa"]
- Università: Università Cattolica del Sacro Cuore di Milano
- Facoltà: Economia
- Esame: Economia industriale
- Docente: Pontarollo Enzo
Altri appunti correlati:
- Microeconomia
- Diritto dell'Impresa
- Riorganizzazioni Aziendali
- Diritto Commerciale
- Economia aziendale
Per approfondire questo argomento, consulta le Tesi:
- Accordi orizzontali: M&A e JV. Il caso Bombardier: analisi di una strategia
- Politica della concorrenza e fusioni orizzontali: analisi di un caso
- M&A DOs and DONTs. Un modello di valutazione ex-ante. Il caso Finmeccanica
- Le concentrazioni tra imprese nel diritto comunitario della concorrenza
- Franchising e normativa antitrust
Puoi scaricare gratuitamente questo appunto in versione integrale.

