Legame dell'ossigeno

Il legame dell'ossigeno alla mioglobina viene descritto dall'equilibrio:
Mb + O2  <--> MbO2
con una costante di dissociazione:       K = [Mb][O2]/[MbO2 ]
La dissociazione dell'O2 dalla Mb può essere caratterizzata dalla sua saturazione frazionale , Υ02, definita come la frazione di siti che legano ossigeno occupati da O2.
 Υ02 = [MbO2]/[Mb]+[MbO2] = [O2]/K+[O2]
poiché l'O2 è un gas, la sua concentrazione viene espressa convenientemente dalla sua pressione parziale, pO2 (chiamata anche tensione di ossigeno). L'equazione precedente può quindi essere espressa come:                                            Υ02 = pO2/K+pO2
Il termine p50 è il valore di pO2 quando la metà dei siti di legame della mioglobina sono occupati dall'ossigeno, cioè quando la saturazione di Υ02 è uguale a 0,50. Dunque K=p50 e l'espressione della saturazione frazionale diventa:                    Υ02 = pO2/p50+pO2
       (equazione valida solo per la mioglobina)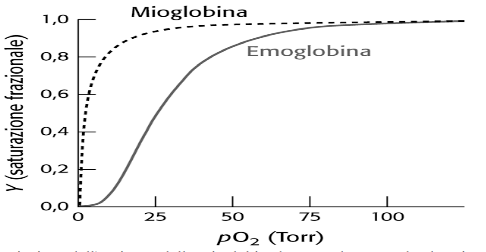



La curva di dissociazione dell'ossigeno dalla mioglobina ha un andamento che descrive una curva di tipo iperbolico, espressa dall'equazione precedente. La Mb modifica di poco la quantità di ossigeno legato anche di fronte a grandi variazioni di pO2; per esempio, con una pO2 di 100 torr la Υ02 è 0,97, mentre per una pO2 di 20 torr la  Υ02 si sposta solo allo 0,88. Al contrario la curva di dissociazione dell'ossigeno dall'emoglobina ha un andamento di tipo sigmoide (a forma di S), infatti, la quantità di ossigeno legato si modifica significativamente anche con una piccola variazione di pO2; per esempio, a 100 torr di pO2 la Υ02 è di 0,95 e diventa 0,30 quando la pO2 scende a 20 torr nel sangue intero. La curva sigmoide della dissociazione dell'ossigeno dall'emoglobina ha un importanza fisiologica fondamentale; essa permette al sangue, infatti, di trasportare più ossigeno ai tessuti di quanto non potrebbe se l'Hb avesse una curva di dissociazione dell'ossigeno di tipo iperbolico, come quella della mioglobina. Comunque, una curva di dissociazione di tipo sigmoide è indicativa della presenza di interazioni cooperative tra i siti di legame di una piccola molecola presenti sulla proteina; cioè i legami di una piccola molecola influenza il legame delle altre. In questo caso il legame dell'ossigeno aumenta l'affinità dell'Hb per il legame delle altre molecole di O2.
I primi tentativi di analizzare la curva di dissociazione sigmoide dell'ossigeno dall'emoglobina furono eseguiti da Archibald Hill nel 1910. Egli considerò una proteina E costituita da n subunità, ognuna delle quali è in grado di legare una molecola di S, che è detta ligande. Assumiamo che il ligande si leghi con una cooperatività infinita:
                                                                    E + nS  <-->   ESn
cioè, la proteina ha tutti i siti (o nessun sito) di legame per il ligande occupati e quindi non possiamo osservare forme intermedie del tipo ES1 o ES2. La costante di dissociazione per questa reazione è:                                               K = [E][S]n/[ESn]
e la sua saturazione frazionale viene espressa, come abbiamo visto prima da:
 ΥS  = n[ESn]/n([E]+[ESn])
Combinando le due equazioni precedenti otteniamo:
                                                            ΥS  =    n[E][S]n/K
                                                            _________________
                                                               n[E](1+[S]n/K)
che dopo riarrangiamento algebrico e cancellazioni di termini diventa:
ΥS = [S]n/K+[S]n
Quest'ultima equazione descrive il grado di saturazione di una proteina multisubunità in funzione della concentrazione del ligande. Comunque, per l'emoglobina, se sostituiamo pO2 a (S), come abbiamo fatto per la mioglobina, l'equazione di Hill diventa:
ΥO2 = (pO2)n/K+(pO2)n
Definendo p50 come il valore di pO2 a cui ΥS corrisponde a 0,50 avremo:
0,50 = (p50)n/K+(p50)n
così che: K = (p50)n
Sostituendo questo risultato all'equazione di Hill per l'emoglobina avremo:
ΥO2 = (pO2)n/(p50)n+(pO2)n
Quindi l'equazione del grafico di Hill per l'emoglobina assumerà la seguente forma:
log(ΥO2/1-YO2) = nlogpO2 – nlogp50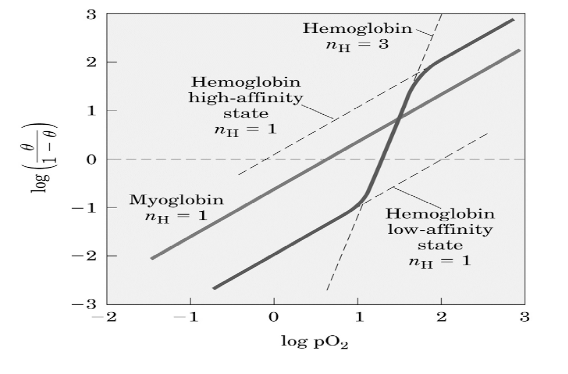



Per la mioglobina, il grafico è lineare con una pendenza, come ci si deve aspettare, pari a 1. Anche se l'emoglobina non lega l'ossigeno in una singola tappa il grafico risulta lineare per valori di YO2 compresi tra 0,1 e 0,9. La sua massima pendenza che si ha quando pO2 = p50(YO2/(1-YO2)), viene considerata come la costante di Hill. Per l'emoglobina umana normale, la costante di Hill sta tra 2,8 e 3,0, e cioè il legame dell'ossigeno all'emoglobina è altamente cooperativo, ma non presenta una cooperatività infinita. A valori di YO2 vicini allo zero, quando sole poche molecole di Hb hanno legato una molecola di ossigeno, la pendenza della retta nel grafico di Hill in quella regione è circa 1 (asintoto inferiore), in quanto le subunità di Hb competono indipendentemente per l'O2, esattamente come le molecole di Mb. A valori di YO2 di circa 1, quando almeno tre dei quattro siti di legame dell'emoglobina sono occupati dall'ossigeno, la retta del grafico di Hill assume di nuovo una pendenza di 1 (asintoto superiore), poiché i pochi siti rimasti vuoti sono su molecole diverse e legano in modo indipendente l'ossigeno. In base all'equazione di Hill e estrapolando l'asintoto inferiore, possiamo notare che è necessaria una p50 di 30 torr per il legame della prima molecola di O2 all'emoglobina. Se ora estrapoliamo l'asintoto superiore, è necessaria una p50 di 0,3 torr per il legame della quarta molecola di ossigeno all'emoglobina. Quindi la quarta molecola di O2 si lega all'Hb con un affinità 100 volte superiore a quella della prima molecola di O2.