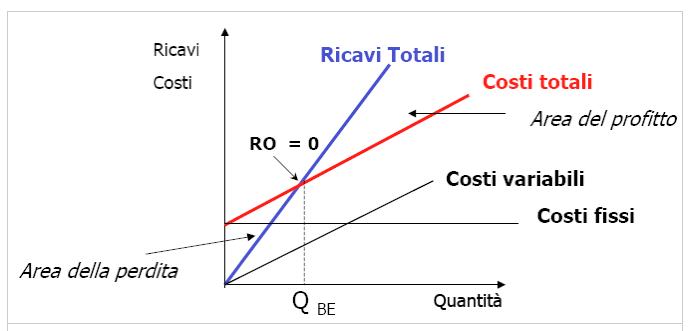
Analisi di break even point
LA RELAZIONE FONDAMENTALE:
Con le ipotesi formulate è possibile costruire la seguente relazione:
RE = P x Q - [ (Cvu x Q) - CF]
RE = ricavi totali - costi totali
RE = (MdCu) x Q - CF
RE = margine di contribuzione totale - costi fissi
dove:
- RE = risultato economico
- P= prezzo unitario di vendita
- Cvu= costo variabile unitario
- Q= quantità prodotte/vendute
- CF = costi fissi
LA RELAZIONE FONDAMENTALE DEL PUNTO DI PAREGGIO:
Ipotizzando un risultato economico pari a zero (pareggio) avremo:
(P-Cvu) x Q - CF =0
Quindi la quantità che garantisce tale risultato (QBE, quantità di break-even) è la seguente: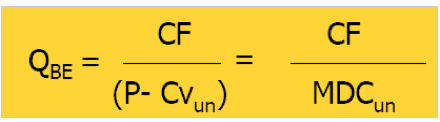
Dalla relazione fondamentale è possibile determinare qualsiasi variabile attraverso le opportune formule inverse:
ESEMPIO:
CF: 100
MDC U: 10
Q BE = 100/10 = 10 – QUOTA DI MDC CHE OCCORRE PER RIUSCIRE A COPRIRE I CF.
Q > 10 = AREA DI PROFITTO
Q < 10 = AREA DI PERDITA
DETERMINAZIONE DI UN RE OBBIETTIVO
Ipotizzando un risultato economico diverso da zero (RE obiettivo) avremo:
(P-Cvu) x Q - CF = RE
da cui, volendo calcolare la quantità che garantisce tale risultato:
Q* = (CF + RE)/(P- Cvu)= (CF + RE) / MDC un
Anche in questo caso è possibile porre come incognita qualsiasi altra variabile della relazione fondamentale ricavando le grandezze che consentono di raggiungere il risultato economico prefissato.
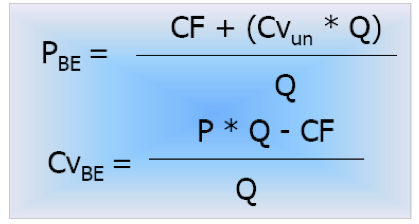
È possibile calcolare il fatturato di pareggio:
E calcolare il fatturato necessario per ottenere un RE predefinito:

ESEMPIO:
CF: 100
MDC U: 10
Q RE OBJ = 100+10 / 10 = 11
Continua a leggere:
- Successivo: Azienda multiprodotto - determinazione del punto di pareggio
- Precedente: L’analisi costi-volumi-risultati - break-even analysis
Dettagli appunto:
-
Autore:
Valentina Minerva
[Visita la sua tesi: "Le strategie di contrasto al fenomeno del riciclaggio: tutela penale e tutela amministrativa"]
- Università: Università Cattolica del Sacro Cuore di Milano
- Facoltà: Economia
- Esame: Programmazione e Controllo
- Docente: Pogna Alberto
Altri appunti correlati:
- Metodologie e determinazioni quantitative d'azienda
- Appunti analisi delle informazioni contabili
- Pianificazione e controllo aziendale
- Macroeconomia
- Fondamenti di economia aziendale
Per approfondire questo argomento, consulta le Tesi:
- L'impatto dei Sistemi di Pianificazione e Controllo nelle PMI
- Il supporto informativo per il controllo di gestione negli enti locali. Il controllo nel comune di Gagliano del Capo
- Il controllo di gestione nelle PMI: il caso GIS S.p.A.
- Il controllo di gestione nelle imprese di assicurazione
- La Metodologia del Business Case - Il Caso Ferrari SpA
Puoi scaricare gratuitamente questo appunto in versione integrale.

