Caratteristiche dell'analisi bivariata

Dopo aver studiato le caratteristiche di ciascun attributo presente in un dataset con le metodologie appena descritte, può essere opportuno analizzare le relazioni tra coppie di attributi.
Nell’analisi bivariata si possono distinguere tre casi:
- entrambi gli attributi sono numerici
- entrambi gli attributi sono categorici
- un attributo è numerico, l’altro è categorico.
Noi considereremo solo il primo caso, a titolo puramente esemplificativo.
L’obiettivo è quello di capire se esiste una correlazione più o meno forte tra una variabile dipendente e indipendenti. È molto più complesso da trattare quando le variabili non sono o non sono entrambe numeriche. Se esiste un legame lineare forte tra due variabili, posso utilizzare uno dei due attributi per la mia indagine.
ANALISI GRAFICA : diagrammi di dispersione
Un diagramma di dispersione rappresenta senza dubbio la rappresentazione più intuitiva del legame esistente tra due attributi numerici.
Consideriamo il seguente dataset (telefonia mobile)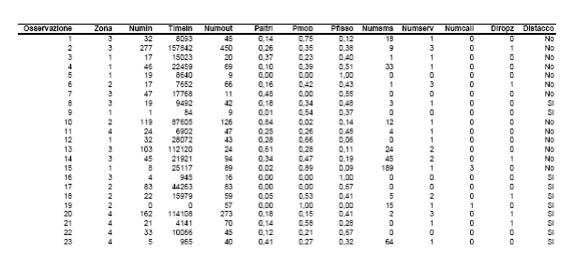


Legenda del dataset (telefonia mobile)


Diagramma di dispersione per gli attributi numin e timein.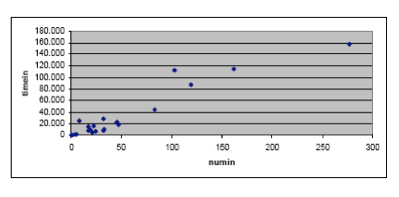


Evidenzia una dipendenza lineare positiva tra i due attributi.
Diagramma di dispersione per gli attributi numin e numsms.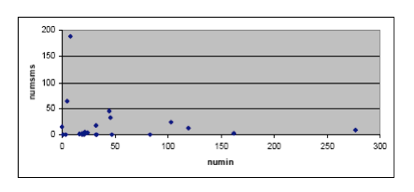


Come era logico attendersi, non evidenzia alcuna significativa dipendenza tra i due attributi.
- INDICI DI CORRELAZIONE ASSOCIATI.
Come nel caso delle analisi univariate, è utile introdurre accanto ai metodi grafici anche indicatori sintetici che esprimono la natura e l’intensità del legame tra attributi numerici.
Il coefficiente di correlazione lineare (r) tra due attributi è una funzione della covarianza e della deviazione standard dei due attributi. La covarianza, a sua volta, è funzione delle medie campionarie dei due attributi.
r è compreso nell’intervallo [-1, 1] ed ha il seguente significato:
r > 0 - Concordanza tra attributi (retta orientata verso l’alto, con approssimazione alla retta tanto maggiore quanto più r si avvicina a 1).
r < 0 - Discordanza tra attributi (retta orientata verso il basso, con approssimazione alla retta tanto maggiore quanto più r si avvicina a -1).
r = 0 - Tra gli attributi non si manifesta alcun legame di natura lineare (le coppie di dati possono disporsi modo del tutto casuale oppure evidenziare un legame di natura non lineare).
Diagramma di dispersione per gli attributi numin e timein e relativo coefficiente di correlazione.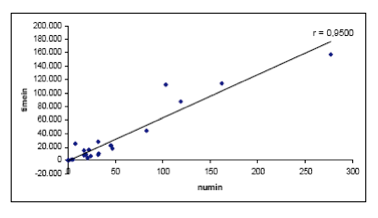


Diagramma di dispersione per gli attributi numin e numsms e relativo coefficiente di correlazione.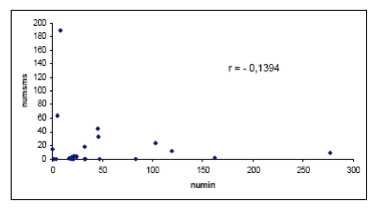

Importanza dell’analisi grafica in un caso emblematico.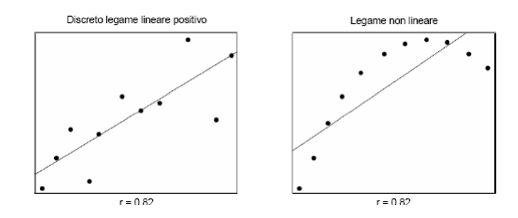




Importanza dell’analisi grafica in un caso emblematico.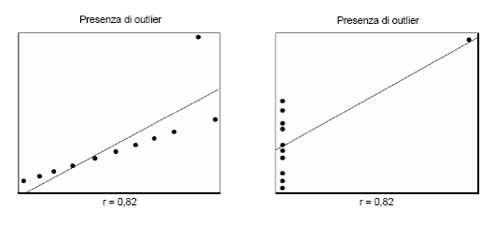



Possono manifestarsi situazioni in cui l’indice di correlazione non è significativo. In questo caso l’indice di correlazione è esattamente lo stesso.

PIATTAFORME DI BUSINESS INTELLIGENCE
Esiste una molteplicità di piattaforme informatiche. Le più note piattaforme proprietarie sono SAS, Microsoft, Microstrategy, Oracle, Ibm/Cognos/SPSS. Ci sono poi piattaforme open source, facilmente scaricabili, come R e Weka.